Overview and Objective
In this lesson, students will use the geared clocks on Polypad to explore the angle patterns on an analog clock. Specifically, they will find the number of times in a day that a clock’s minute and hour hands overlap to form a straight line.
Warm-Up
Invite students to open a blank canvas and use the geared clock to adjust so that the clock’s minute and hour hands form a straight angle.
Although students can come up with different answers, the obvious answer is 6 o'clock. Clarify with the students that for a.m /p.m mode, that are two different times a day for 6 a.m and 6 p.m. In 24 hours mode, that is 6:00 and 18:00.
Therefore in a 24-hour day, we already found two examples of times that the minute and hour hand create a angle.

You may suggest students use the toggle seconds option at the bottom center toolbar after selecting a clock on the canvas to hide and show the second hand.
If the students found the other straight angles, let them share their answers by recording those times on a board. If not, ask them to move the minute hand slowly to observe the other times that create angle. Discuss with students that it is not easy to tell the time precisely that creates the straight angle other than 6 a.m and p.m.
Main Activity
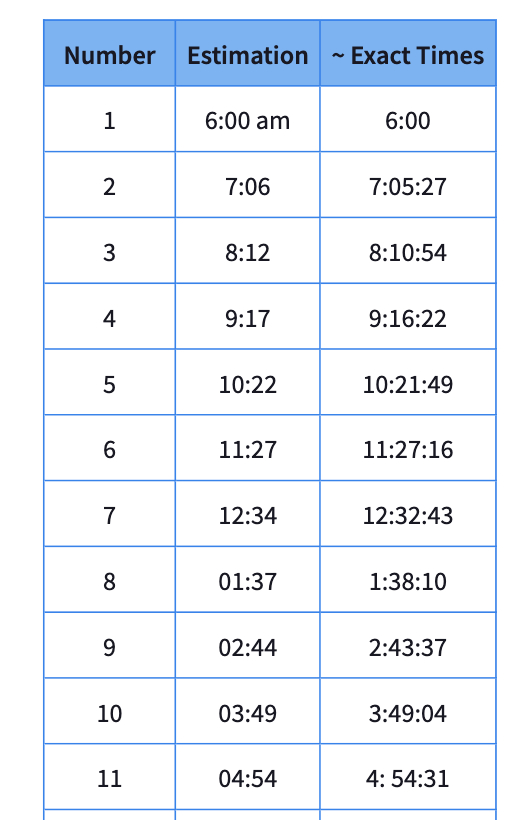
Using the table tool, have students record all possible times with angle (between 6 a.m and 6 p.m). Students may also use the protractor tool if they need it. However, remind them they do not need to be precise here since they are actually looking at the number of times that hands form a straight angle rather than the actual time. Approximation for each time is enough.
Here are some possible answers.

Students could talk about patterns they notice, such as
- In 12 hours, there are 11 times they can observe a straight angle.
- After 6 a.m, almost every 65 minutes, they see a straight angle.
Here they can use their observations to create an equation to find the exact times.
11 equal parts in 12 hours mean 11 equal parts in 720 minutes. It means, in every
= minutes (which is very close to their estimation), they can observe a straight angle on an analog clock. While intuition might tell us that there should be 24, we proved that there are 22 times a day a straight angle can be observed the clock.
They can also find the exact times by adding 65 minutes to 6:00. To make the calculations easier, we can express each interval as 65 and minutes which is
= 65.454545454.. minutes = 1h 5min 27.272727..seconds
Another approach to finding times can be using the unit rates.
Clarify with students that the minute hand coves 360 degrees (makes a full turn) in 60 minutes. Discuss the speed of minute hand in degrees per minute. The hour hand covers 360 degrees in 12 hours (= 720 minutes), and ask about the speed of hour hand in degree per hour and minute.
The speed of the minute hand is 6 degrees per minute, whereas the speed of the hour hand is 30 degrees per hour which means degrees per minute.
We know that at 6:00, both are at the same position but will now move at different speeds.
The relative speed between the minute and hour hand = degree per minute.
They will create another straight angle when the relative speed between them covers 360 degrees.
Therefore in every which means minutes, they will create another 180-degree angle.
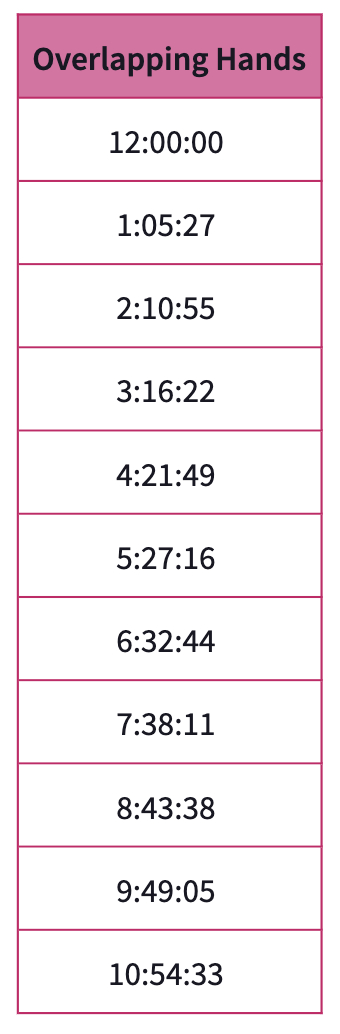
In the second part of the lesson, after discussing the relative speeds of the hour of minute hands, you can ask about how many times a day the hour and minute hand overlaps?

Again start with the most obvious one, which is 12 o'clock. Let them use different clocks to show each time with overlapping hands.

Closure
Invite a different student to share each time with the overlapping hands. To close the lesson, ask students to try to find the exact times with the overlapping hands. They may write the times over a 12-time period then convert to a.m /p.m versions.
Polypads for This Lesson
In this activity, students can use blank canvasses by inserting geared clocks. Here are the canvasses for teacher use only.