Lesson outline
This task uses Polypad’s tetrominoes as a context for exploring enlargements (dilations) and scale factors. Tetrominoes are shapes which can be made from 4 individual squares, and will be instantly recognisable to any student who has played the classic game Tetris.
Lesson objective: Understand how the area of a shape changes when it is enlarged.
Lesson activity
Warm-up
Show students this Polypad canvas. Explain that two of the tetrominoes have been enlarged (dilated) correctly, but two of them have mistakes. Invite students to work out the scale factor by which the two correct enlargements have been drawn, and to use the pen tool (or copy the diagrams onto squared paper) to correct the mistakes in the incorrect enlargements.
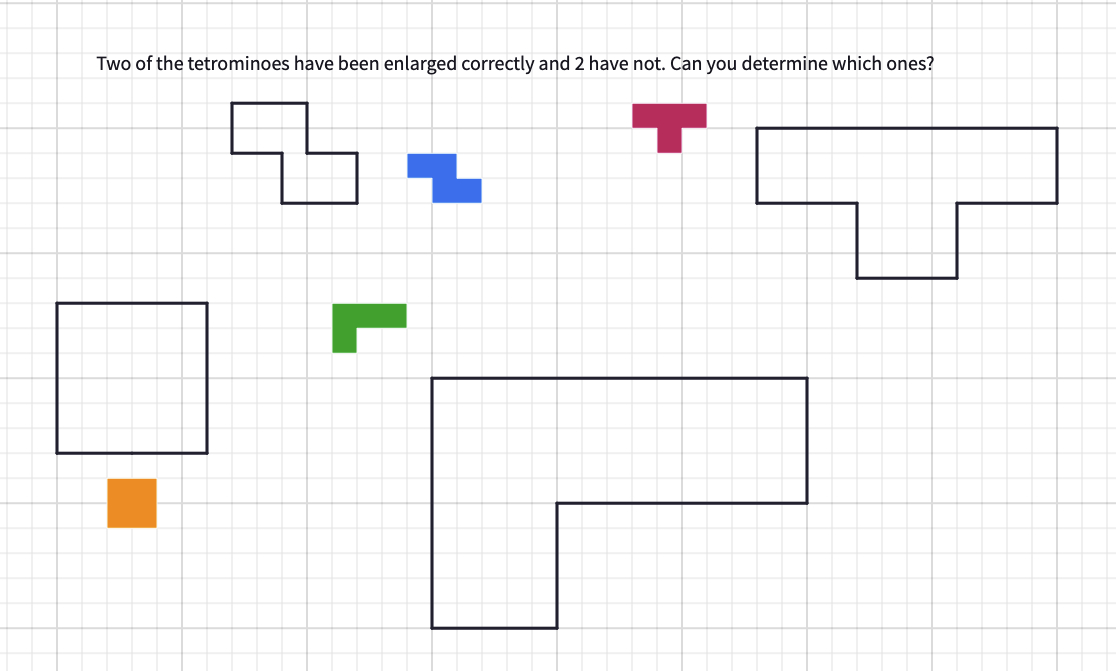
Solution: The square has been correctly enlarged by a scale factor of 3, and the L tetromino has been correctly enlarged by a scale factor of 5. The T tetromino and the Z tetromino have not been enlarged correctly.
If students haven’t seen tetrominoes before, and you think they could benefit from additional scaffolding before the warm up above, you could challenge them to find all the different arrangements of four 1-square tiles. They can use this canvas as a starting point.
Main Activity
Some shapes can be used to tile an enlargement of themselves – this is sometimes called a rep-tile. In this activity, students will explore how the L tetromino can be tiled to make enlargements of itself.
First, invite students to draw enlargements of the L tetromino by a scale factor of 2, 3, 4 and 5, using the pen tool. Students should enable the grid background using the grid button on the right.
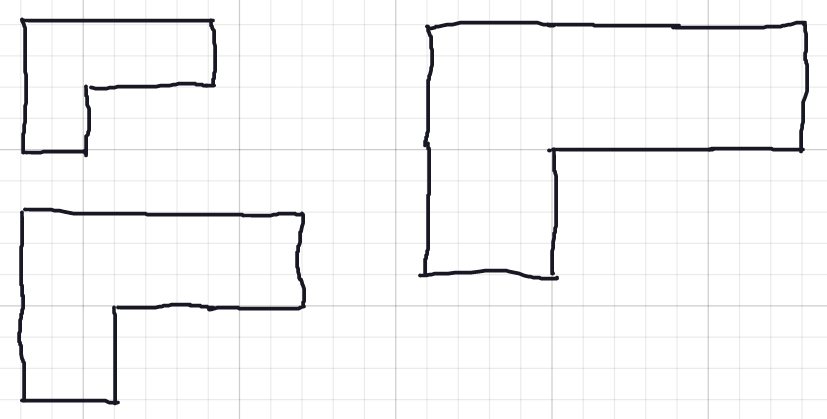
Next, challenge your students to fill each of these outlines using copies of the green L, without any gaps or overlaps!
If students are struggling, you can relax the constraints and allow them to use a mixture of different tetrominoes. Since all tetrominoes have the same area, this won’t affect the following questions.
There are many different possible solutions, but here are some examples:
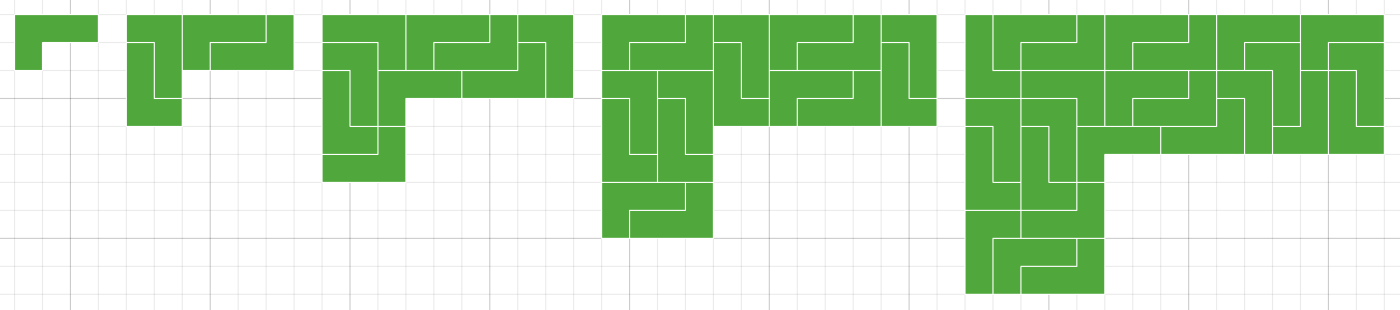
Once students have completed some tilings, ask them to record how the area changed for each shape they have tiled. Students could record their results in a table, like the example below. Consider whether your students could benefit from receiving a blank copy of the table to fill in.
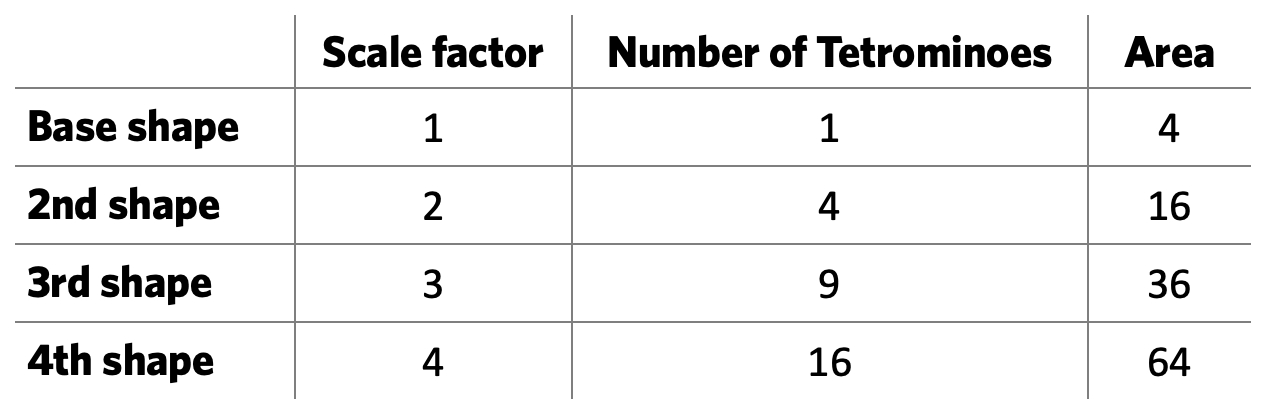
It may not be immediately obvious to students that the area of each shape is four times the number of tetrominoes used, since each tetromino has an area of four. Make sure this emerges during any class discussion.
Once students have recorded their findings, bring the class together and share results. Invite them to say what they notice about the number of tetrominoes needed and the area of the new shape. Students might observe that the number of tetrominoes needed in the enlargements is always a square number, as is the area of each shape.
Encourage students to justify their findings by thinking about how area is a two-dimensional quantity so if the length and the width of a shape have each been enlarged by a factor of n, the area has increased by a factor of n in each dimension so the area is multiplied by . In this example, the starting area is 4, so the area of the nth shape is . Students might add this final row at the bottom of their table:

Support
Students who are having difficulty getting started with the task can just focus on drawing enlargements that can be tiled using the square tetromino, or using combinations of multiple tetrominoes.
Before focussing too much on the area, invite students to consider what they notice about the number of tetrominoes needed to make enlargements of different sizes. The results should be the same as above.
Possible extension
Once students have successfully filled in all enlargements of the L tetromino, you can challenge them to create similar enlargements and rep-tiles consisting of other tetrominoes.
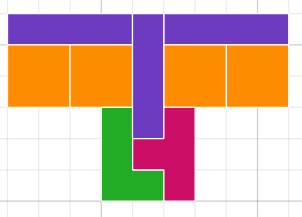
They might notice that while any integer-sized enlargement of the L tetromino can be tiled using small copies of the L tetromino, this is not true for all the others. For example, some but not all enlargements of the T tetromino can be rep-tiled:
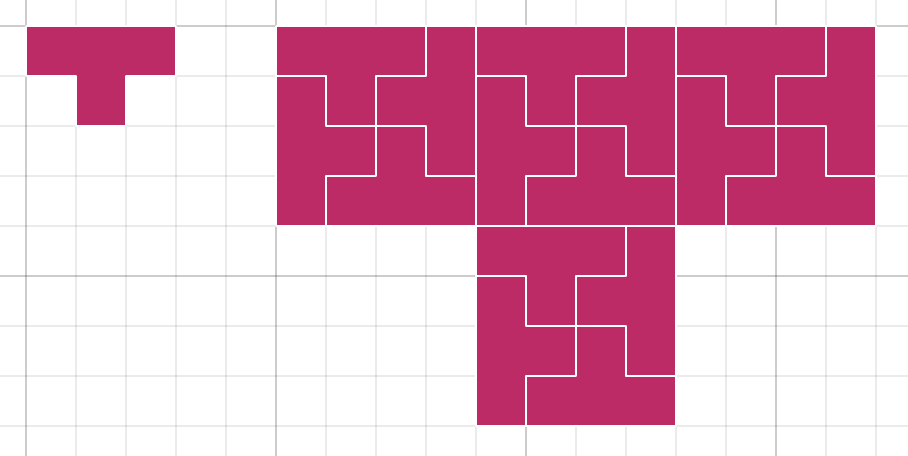
Students can also explore how to tile much larger copies of the L tetromino. Some generalisations can be made by using what we already know to work out what else we can tile. For example, you could challenge students to consider how they could use their answers to enlarging by a scale factor of 3 and scale factor 2 to work out how to tile the enlargement with scale factor 6. It is possible to prove that every enlargement of the green L can be tiled.
Finally, rep-tiles can be created not just using the five tetrominoes but also using other polygons. For example, here you can see rep-tiles of trapeziums (on an isometric grid):

Which other shapes can students enlarge and fill in this way? For more advanced students, this could even lead to a discussion of Fractals (e.g. the Sierpinski triangle).